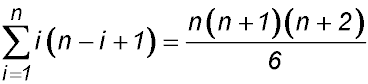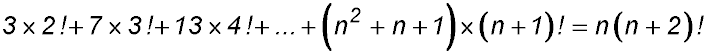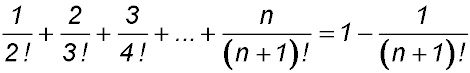Prove the following relationships true for all natural numbers ≥ 1.
| Basic series with integers. |
1. |
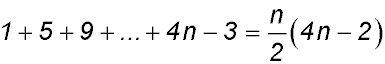
For S(1): LHS = 1 and RHS  ∴ true ∴ true
∴ true for n = 1.
Assume true for n = k.
So S(k) = 1 + 5 + 9 +...+ 4k - 3 =  . .
Try n = k + 1
Required to prove S(k+1) = 1 + 5 + 9 +...+ (4k-3) + 4k + 1 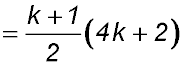
LHS  + (4k + 1) + (4k + 1)
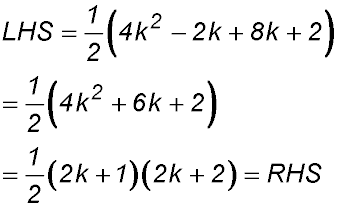
∴ true by mathematical induction for n ≥ 1. |
| |
2. |
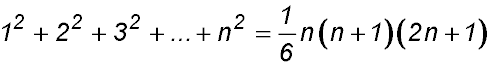
For S(1): LHS = 1 and RHS 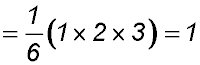 . ∴ true . ∴ true
Assume true for n = k
So S(k): 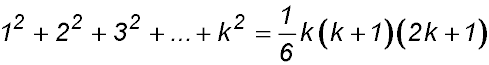
Required to prove S(k+1) = 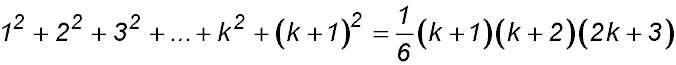
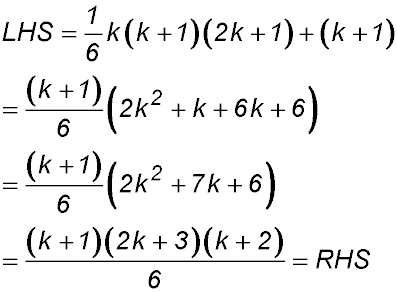
∴ true by mathematical induction for n ≥ 1. |
| |
3. |
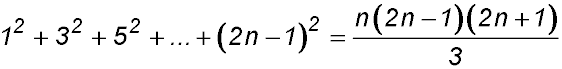
For S(1): LHS = (2×1-1)2 = 1 and RHS  ∴ true ∴ true
Assume true for n = k
So S(k): 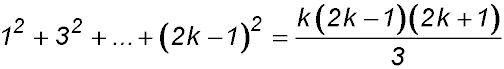
Required to prove S(k+1):
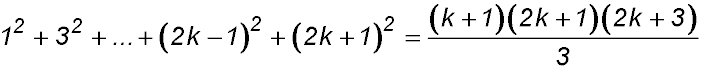
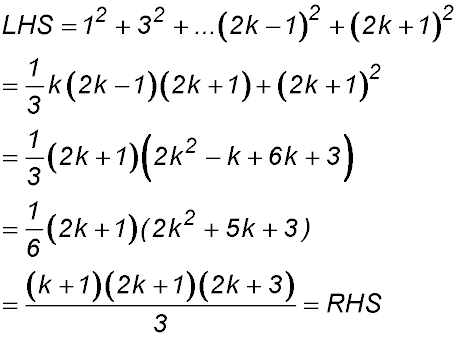
∴ true by mathematical induction for n ≥ 1. |
| |
4. |
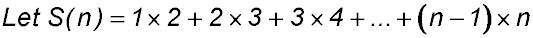 . .
Use mathematical induction to prove that, for all integers n ≥ 2.
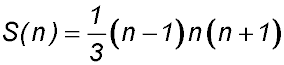
For S(2): LHS = 2 and RHS 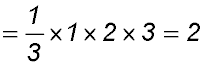 ∴ true ∴ true
Assume true for n = k
So S(k): 
Required to prove S(k+1) =
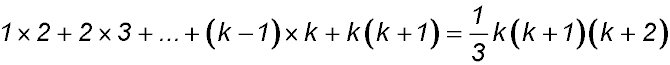
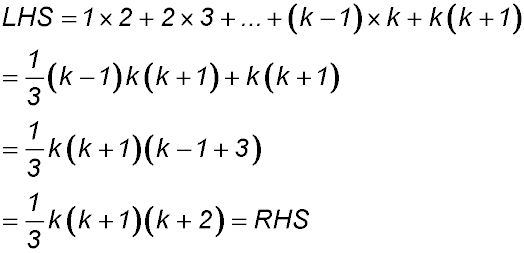
∴ true by mathematical induction for n ≥2. |
| |
5. |
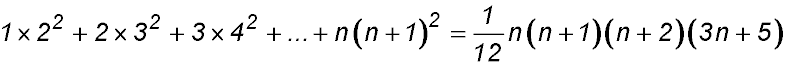
For S(1): LHS = 4 and RHS 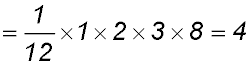 ∴ true ∴ true
Assume true for n = k
So S(k): 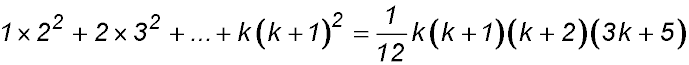
Required to prove S(k+1):
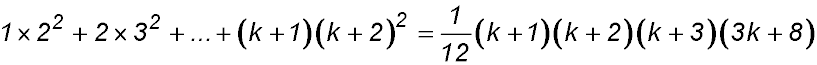
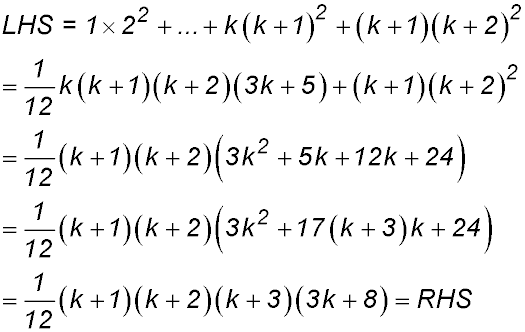
∴ true by mathematical induction for n ≥1. |
| |
6. |
Now make up your own induction questions of this type.
Take any arithmetic or geometric series you have dealt with,
find its sum in the usual way and then prove it by induction. |
| Fractions. |
7. |
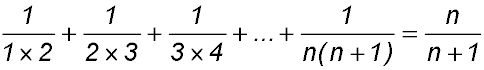
For S(1): LHS = 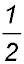 and RHS = and RHS = 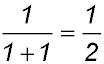 ∴ true ∴ true
Assume true for n = k
So S(k): 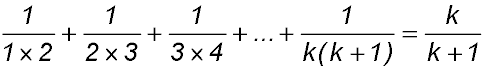
Required to prove S(k+1):
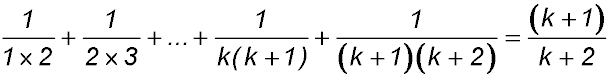

∴ true by mathematical induction for n ≥1. |
| |
8. |
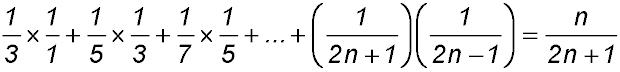
For S(1): LHS =  and RHS = and RHS = 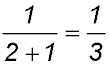 ∴ true ∴ true
Assume true for n = k
So S(k): 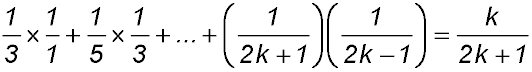
Required to prove S(k+1):
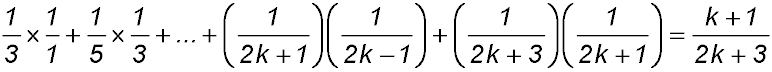
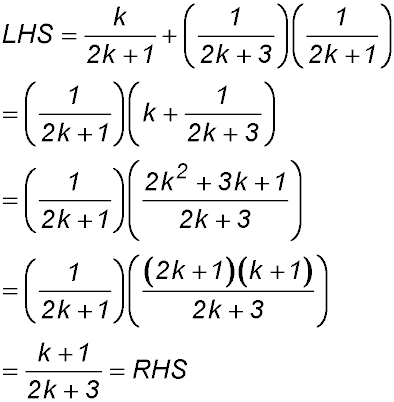
∴ true by mathematical induction for n ≥1. |
| |
9. |
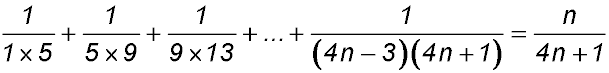
For S(1): LHS = 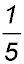 and RHS = and RHS =  ∴ true ∴ true
Assume true for n = k
So S(k): 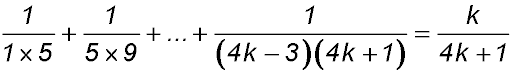
Required to prove S(k+1):

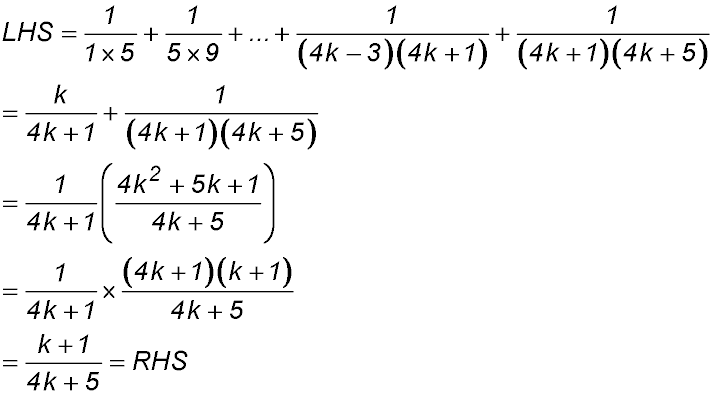
∴ true by mathematical induction for n ≥1. |
| Sigma notation. |
10. |
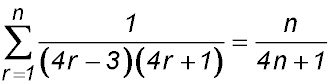
For S(1): LHS = 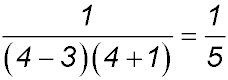 and RHS = and RHS = 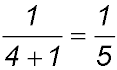 ∴ true. ∴ true.
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| |
11. |

For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| |
12. |
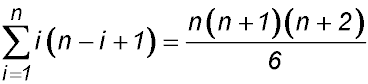
For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| Factorials. |
13. |

For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| |
14. |
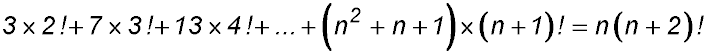
For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| |
15. |
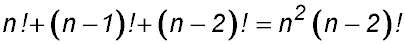 for n ≥2. for n ≥2.
For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
| |
16. |
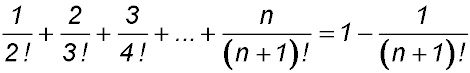
For S(1): LHS = 1 and RHS ∴ true
Assume true for n = k
So S(k):
Required to prove S(k+1) =
∴ true by mathematical induction for n ≥1. |
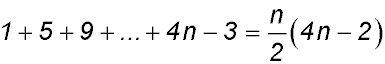
 ∴ true
∴ true .
.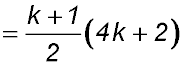
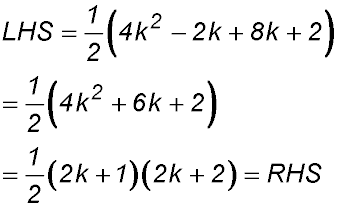
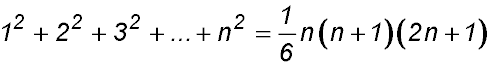
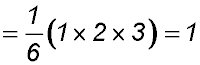 . ∴ true
. ∴ true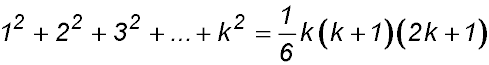
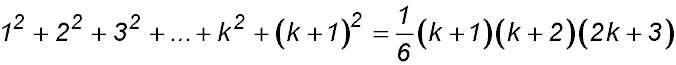
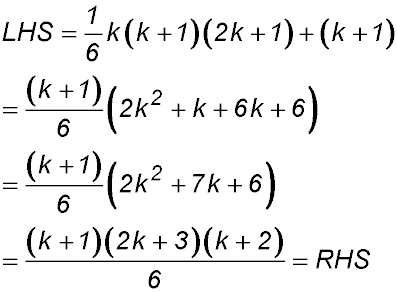
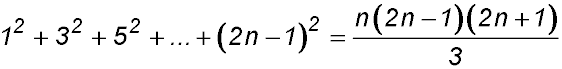
 ∴ true
∴ true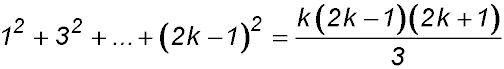
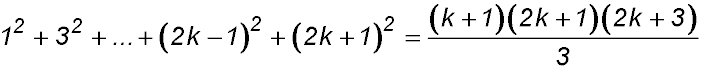
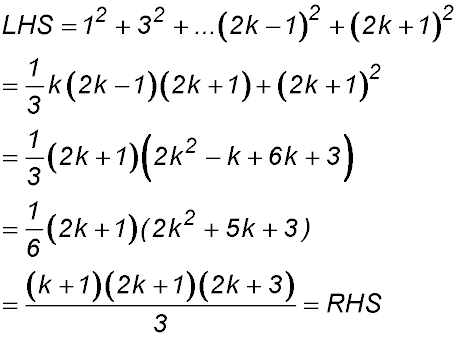
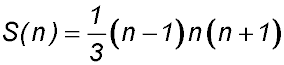
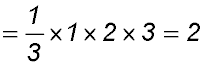 ∴ true
∴ true
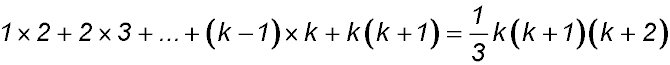
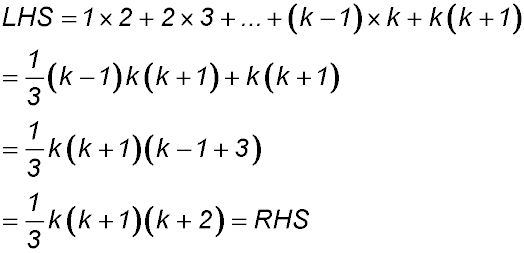
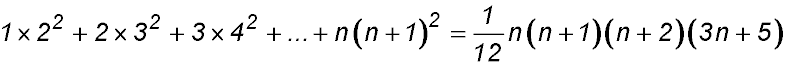
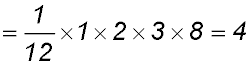 ∴ true
∴ true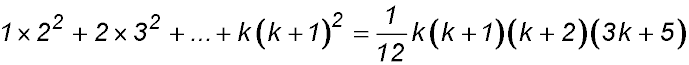
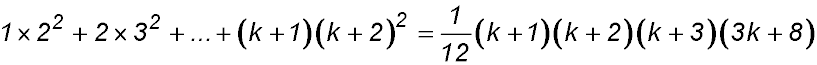
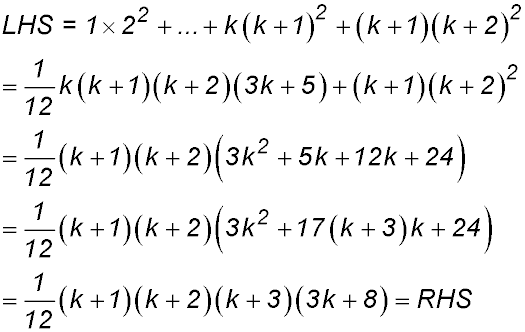
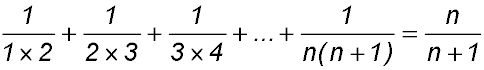
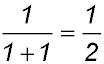 ∴ true
∴ true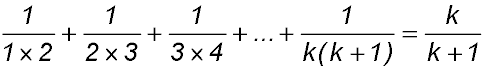
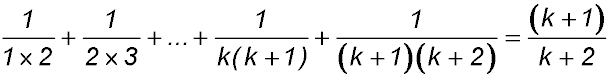

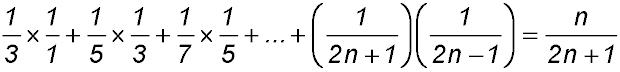
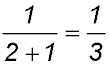 ∴ true
∴ true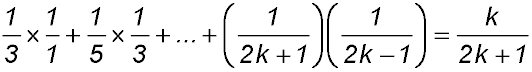
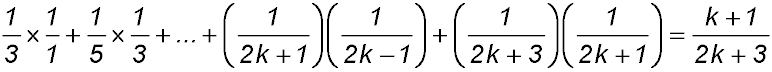
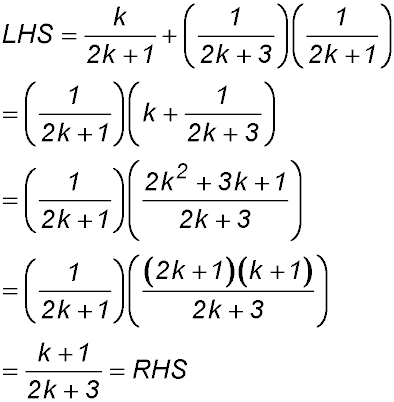
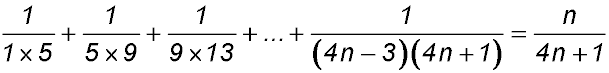
 ∴ true
∴ true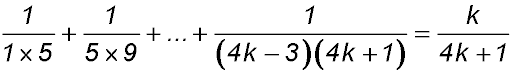

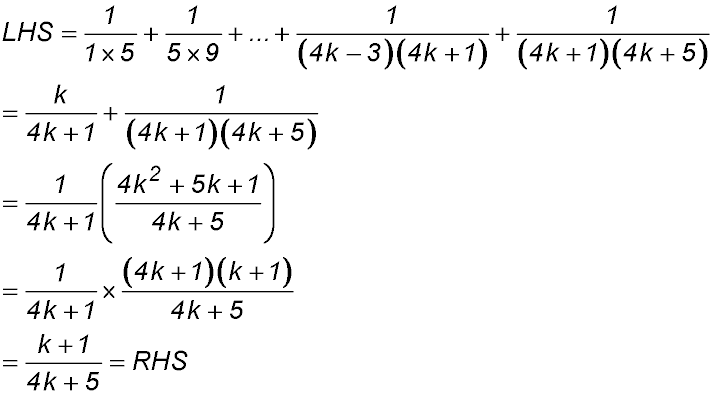
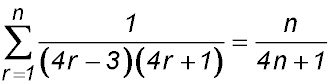
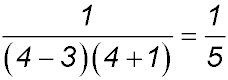 and RHS =
and RHS = 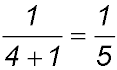 ∴ true.
∴ true.